Batch 2 - Class 299 - Pascal's Triangle II
zoom: send meeting Id and password
Start recording
Preclass Exercise:
Attendance: Raghav, Anika, Aneesh, Tarush, Vansh, Yatharth, Rhea Chadha, Ryan Chadha, Advay, Vivaan, Adyant, Ayush, Nikhil, Aarav, Aarushi, Ekagra, Dhriti
Class Notes: (repeat from class 221)
Review of the arcade game and patterns already discussed

- Any number is equal to the two numbers above it
- The triangle is symmetric around vertical axis
- There seem to be powers of 11 on each row
- Total each row of Pascal's triangle and see the pattern. What can we say about nC0+nC1+...nCn?
- In last class, we did the hopper game, and saw similar chances of the hopper landing at a particular position. why? Can you draw the correspondence between our marble path here, and the hopper game? (Hint: Consider what positions are in play after each step and map them to Pascal's triangle)
.png)
- Lets draw this slightly differently and see more patterns
.png)
- Lets look at the pattern along an edge
- First edge 1,1,1,1,1
- Second edge 1,2,3,4,5,6 (counting numbers)
- Third edge 1,3,6,10... - what are these? Triangular numbers (illustrate)
- What do successive triangular numbers total to? Can you think why?
- Fourth edge 1,4,10,20,35... - what are these? Tetrahedral numbers (illustrate)
- Fifth edge 1,5,15,35,70... - can you guess what might these be? Yes, pentatope numbers - number of vertices in a 4-D "triangle"
- Hockey Stick Pattern - Example 1+3+6+10+15 = 35 - Why?
- Parallelogram Pattern - Example - the whole block from left top to 21, totals to 84 - Why? Successive Hockey sticks!
- Lets try one more way of drawing it

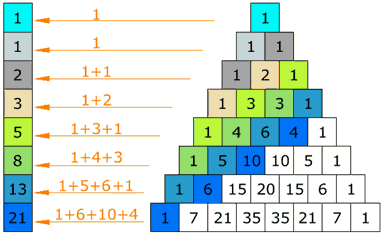
- What are the diagonal totals? Does anyone recognize these numbers? Can you think why?
- Can you spot them on the original Pascal triangle?
- Make a pattern by going up and then along to right, and so on. What pattern do we get? why?
- Sierpinski Triangle - color all the odd numbers on pascal's triangle and see what happens (may need a large pascal's triangle)
- If you keep going, you get the following pattern
- Now color all multiples of 3 in one color and all numbers one greater than multiple of 3 in another color
- There are several other advanced patterns hidden in Pascal triangle - such as value of e, pi, star of david, catalan numbers...
Homework
- In how many ways can you distribute 10 identical balls into 4 distinct bags colored red, yellow, orange and green. You may place any number of balls in each bag, or leave a bag empty
- Answer: Consider the words formed by 10 B's and 3 P's (P being a partition where one bag ends and the next begins) - 13C3
References: